PR JECT

AN EXTENSION OF MARTIN GARDNER CARD TRICK
Gardner's Problem Solver
The number of dealing piles (M)
The number of cards in each pile (N)
The number of dealing rounds (K)
 
Abstract

Martin Gardner’s card trick is a classic mathematical card trick, using number base and ordering to create the magic. This trick lets the inspector memorize a random card and point, after dealing cards into many piles, at the pile that has that card; the process of dealing cards and pointing a pile is repeatly performed; then, the chosen card will finally be at the given position. Since Martin Gardner's card trick and other related card tricks may not be practicable in some situations, it is interesting to find the conditions that make this card trick solvable as well as the ways to perform the trick. This card trick has 3 parameters: the number of piles, the number of cards in each pile and the number of rounds to restack the piles. In this project, we provide an instant program which can tell whether a Gardner's problem with given parameters is solvable or unsolvable. Moreover, for a solvable problem, all possible ways to perform the Gardner's trick are provided. Some anticipated conditions on the parameters that make the Gardner's problem solvable or unsolvable are also given.

Martin Gardner's Card Trick

In Mathematics, Magic and Mystery, Martin Gardner evolved Gergonne 3-pile problem to the 27-card trick. Playing the trick, let a spectator selects any card in a deck of 27 cards, memorizes it and shuffles the deck as much as desired.

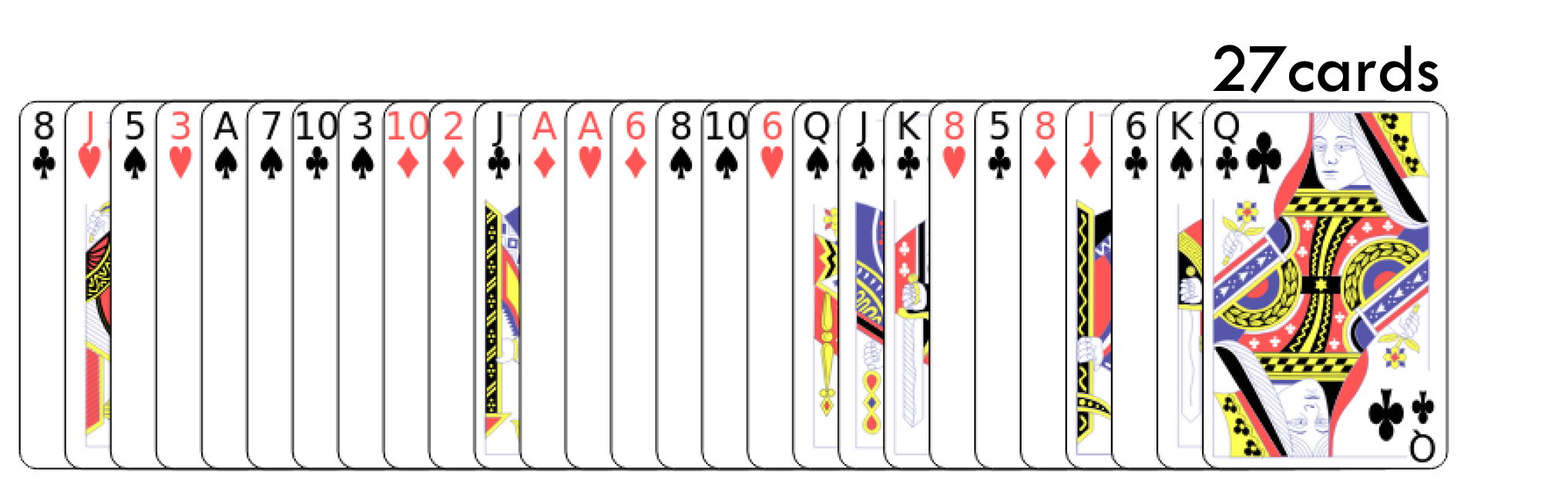
The spactator will choose the position 1-27 of the deck. The magician create three face-up piles of nine cards by dealing the top cards respectively onto the left, middle, then right pile and repeating until all the cards are gone.

Now, he gets 3 piles of cards. Next, the participant points to which pile contains the chosen card.

After that, the magician gather all those piles and put the chosen pile to the specific order. The problem involves distributing these cards with 3 piles and 3 times assembly. Finally, the magician can make the desire position be the chosen card.

Mathematics Behide 27-card Trick

Performing the 27-card Gardner’s trick depends on base three arithmetic. First, we subtract the desired position chosen from the spectator by 1 and convert that resulting number into a three digit number in base 3. We will call this base-3 number a “code”. Next, we decode each digit in the code starting from right to left to perform the Gardner’s trick in each round by placing the indicated pile (from the spectator) in the interpreted position. If the digit is 0, the chosen pile goes on top (none above it); if it is 1, the chosen pile goes at the middle (one stack above it); if it is 2, the chosen pile goes at the bottom (two stacks above it). Performing the trick according to this strategy will finally bring the chosen card to the desired position. This table shows all corresponding pairs of desired positions and codes for performing.

Position 1 2 3 4 5 6 7 8 9
Code 0003 0013 0023 0103 0113 0123 0203 0213 0223
Position 10 11 12 13 14 15 16 17 18
Code 1003 1013 1023 1103 1113 1123 1203 1213 1223
Position 19 20 21 22 23 24 25 26 27
Code 2003 2013 2023 2103 2113 2123 2203 2213 2223
Some Definitions and Theorem

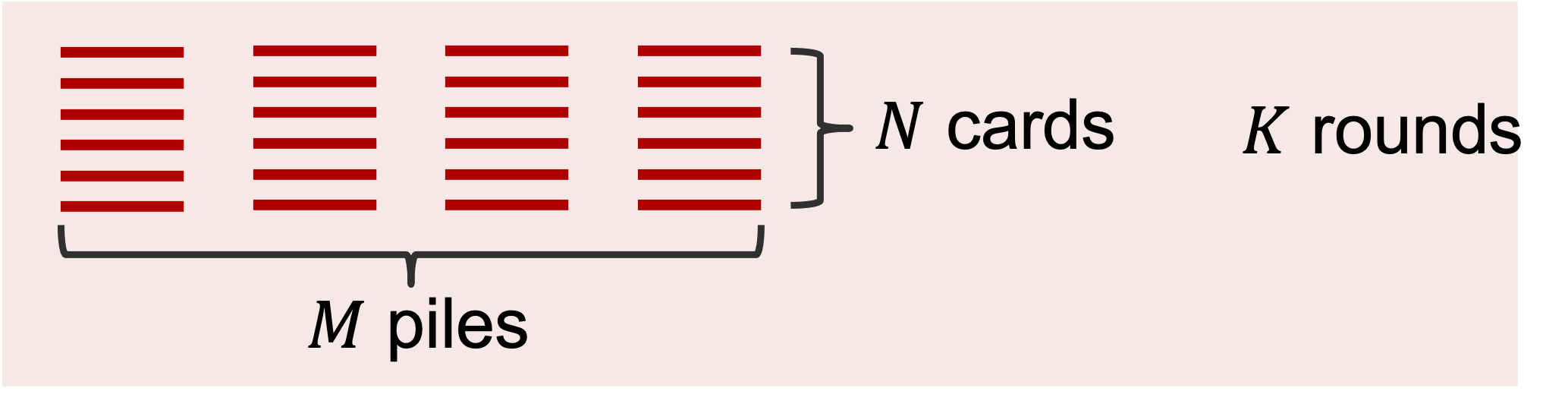
Definition For a Gardner’s problem, we define parameters M, N, K as follows:
  M is the number of dealing piles in each round,
  N is the number of cards in each dealing pile, and
  K is the number of dealing rounds.

Definition For a Gardner’s problem with given parameters M, N, K, let x be the desired position chosen by a spectator at the beginning of the performance.

Our Program

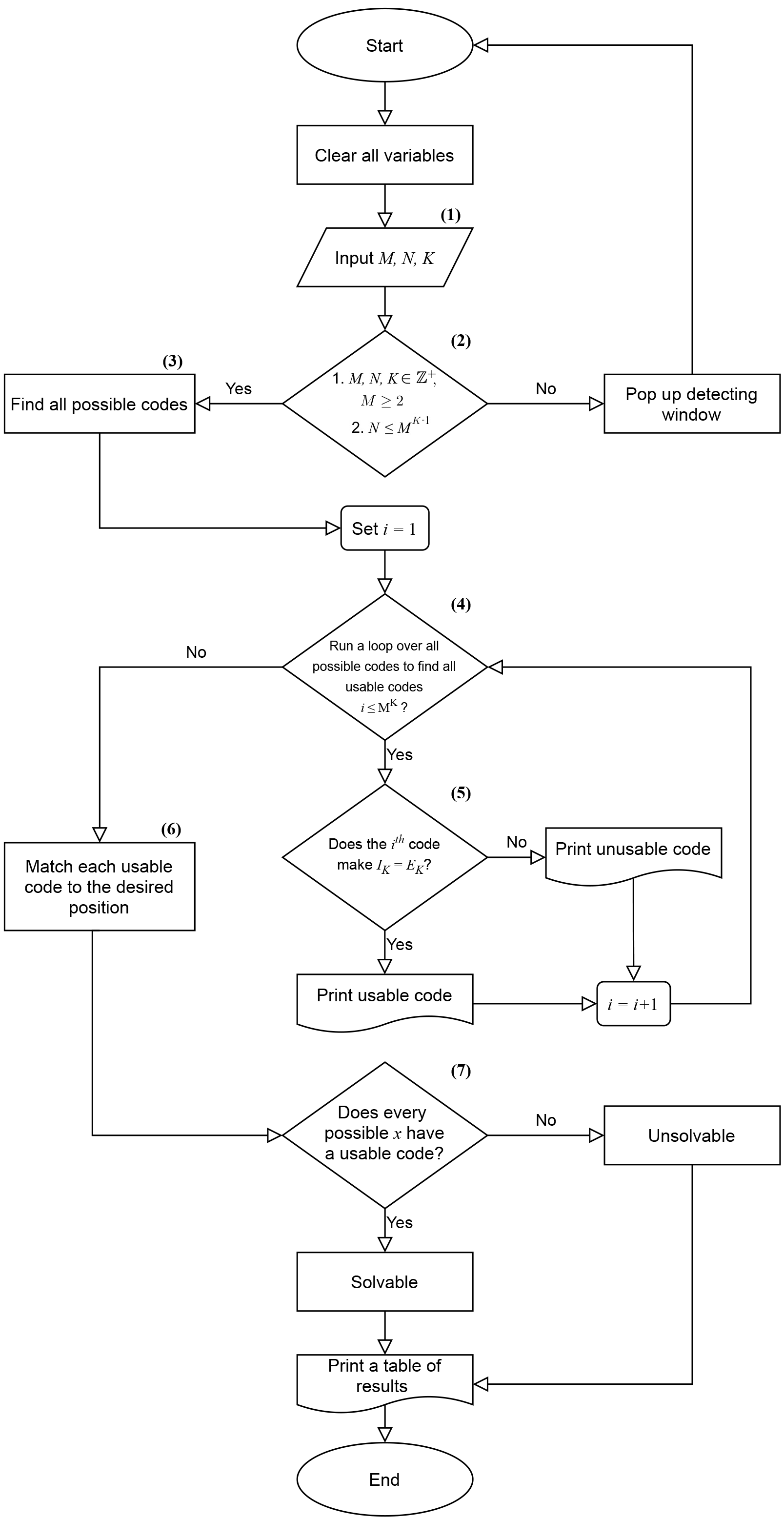
We make an instant program using Mathematica which can tell whether a Gardner’s problem with given parameters is solvable or unsolvable. Moreover, for a solvable problem, the program can show all possible ways to perform the Gardner’s trick.

  1. Input parameters M, N, K.
  2. Check the conditions on parameters M, N, K.
  3. Create all possible M K codes to perform.
  4. Run a loop over all possible codes to find all usable codes.
  5. Classify usable and unusable codes using Corollary check whether IK = EK .
  6. Match each usable code to the corresponding desired position x = IK .
  7. Check whether the Gardner’s problem is solvable or not and show the result.
Results

Example For parameters M = 4, N = 13, K = 3, the Gardner’s problem is unsolvable. We can see that only position x = 1, 5, 9, 13, 14, 18, 22, 26, 27, 31, 35, 39, 40, 44, 48, 52 can be performed.

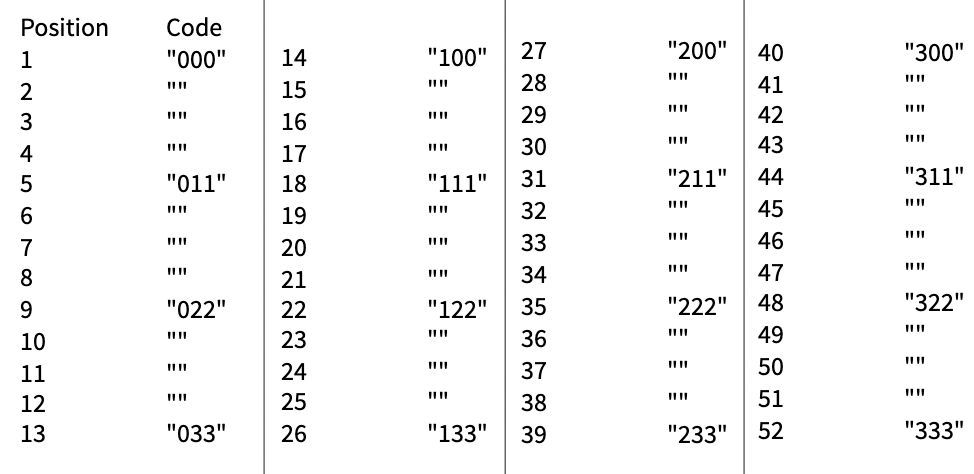
Example For parameters M = 4, N = 13, K = 4, the Gardner’s problem is solvable. We can see that every desired position has corresponding codes to perform. Note that we can have more than one usable code for a desired position. For example, the desired position x = 33 has 4 usable codes which are 2200, 2201, 2132, 2133 in base-4.

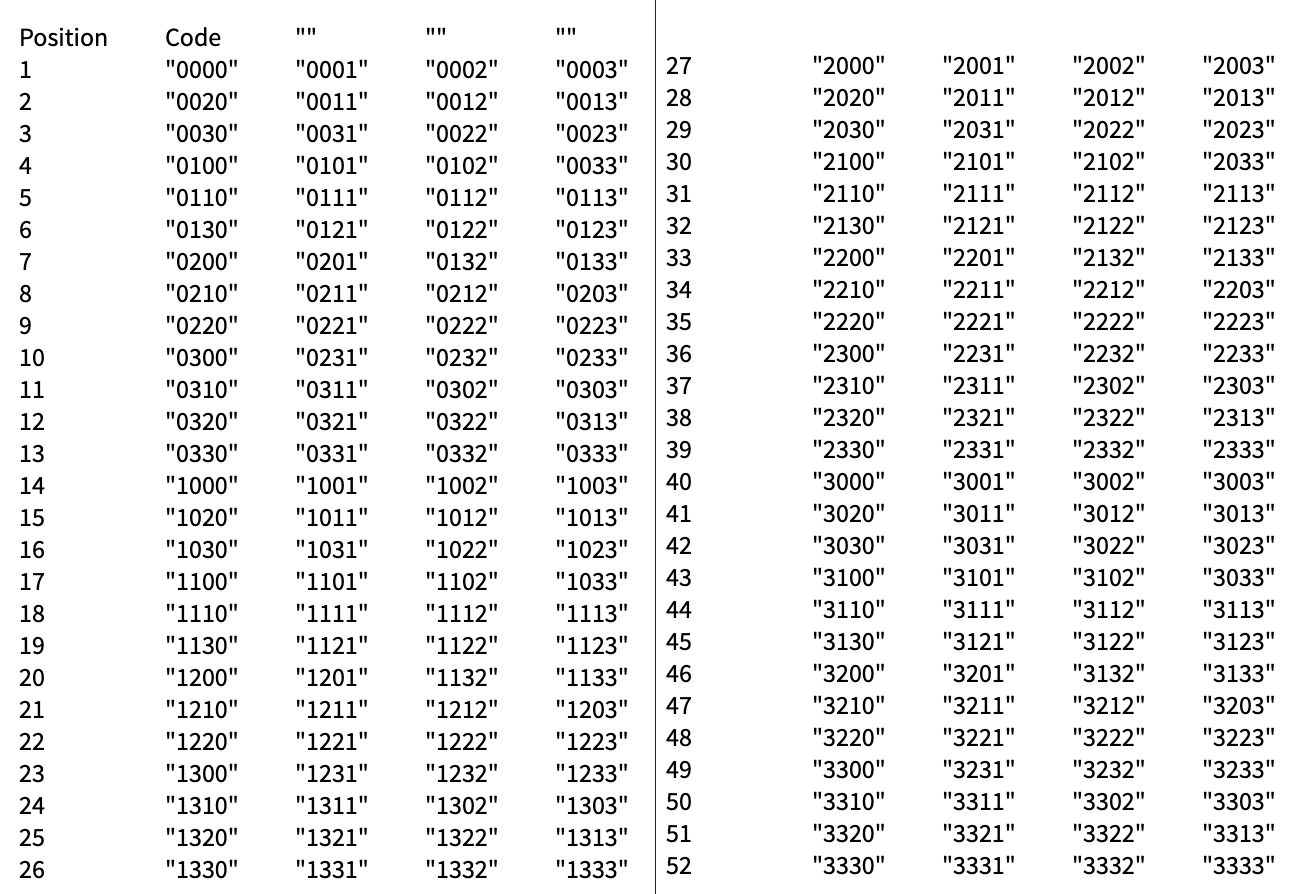
Conclusion

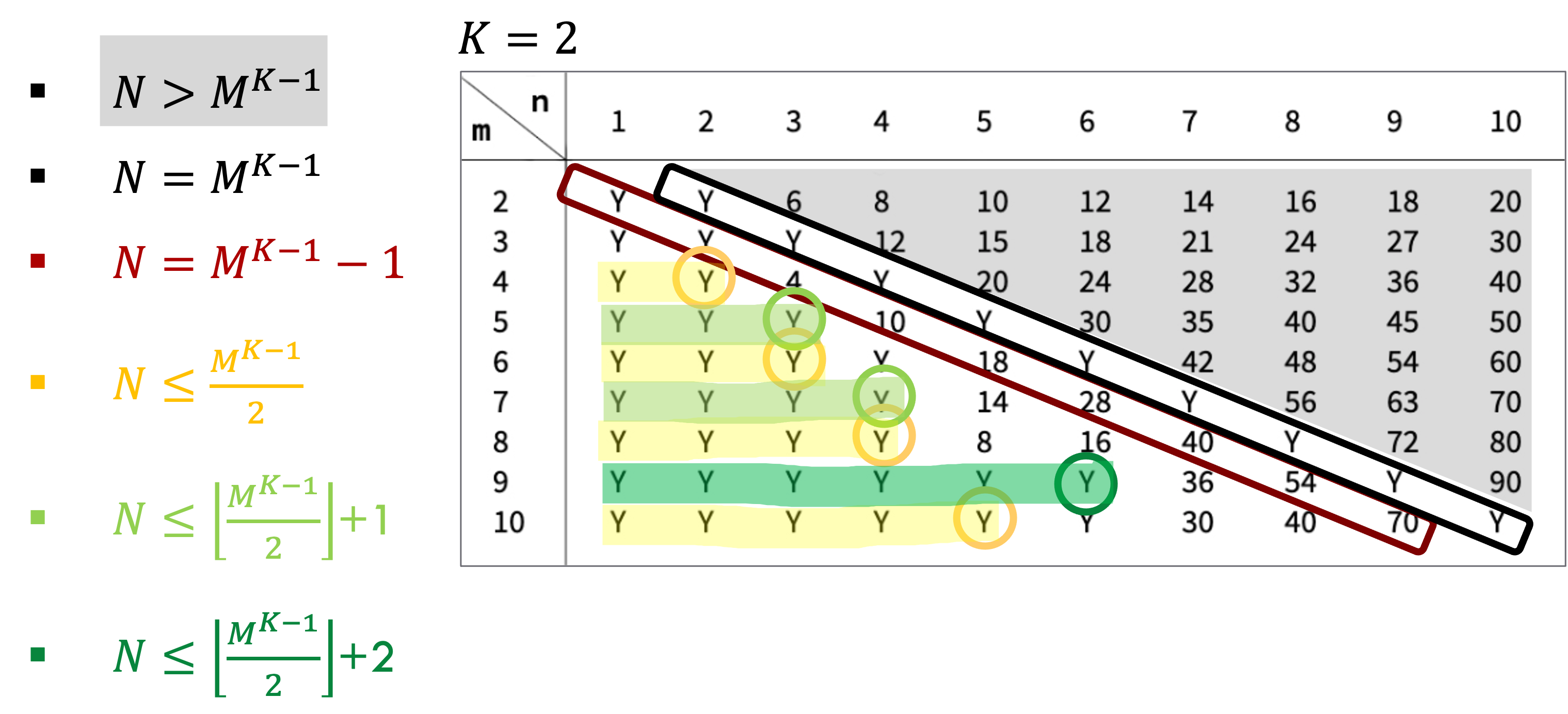
In this work, we provide an instant program as a tool to study Gardner’s problem. The program can tell whether a Gardner’s problem with given parameters is solvable or unsolvable. For a solvable problem, all possible ways to perform the Gardner’s trick are also provided. We also simulate some experiments of the Gardner’s problem with some parameters M, N, K. From the result, for any M, N, K ∈ N, M ≥ 2, we can conclude conditions for the parameters that make the Gardner’s problem solvable or unsolvable as follows.

  1. N > MK−1 The Gardner’s problem is unsolvable. We conjecture that the number of unusable positions in each case is MN.
  2. N = MK−1 Gardner’s problem is solvable. Furthermore, we know a way to perform the desired position x by converting x − 1 to base M as a K digit performing code.
  3. N < MK−1. From our experiments, we conjecture the following results.
    • If N = MK−1 − 1, then the Gardner’s problem is unsolvable. Moreover, the number of unusable positions in such case is M(MK−1 − 3), for every MK−1 ≥ 3.
    • If M is an even number and N ≤
      MK−1 / 2
      , then the Gardner’s problem is solvable.
    • If M is an odd number and N ≤
      MK−1 / 2
      + 1, then the Gardner’s problem is solvable. Moreover, if M is divisible by 3 and N ≤
      MK−1 / 2
      + 2, then the Gardner’s problem is solvable.

Discussion

For 

MK−1 / 2
< N < MK−1, most sets of parameters M, N, Kare unsolvable. However, there are some interesting cases that are solvable. The relationship condition that makes those sets of parameters solvable still remains open for future works.

Although we have an easy way to perform the Gardner’s trick for a deck of size nk, we did not study about how to perform the trick for a person in real life when we actually get the desired position from a spectator, since we need a computer to tell us the code to perform. We hope that this instant program and our anticipated conditions can be useful to study the Gardner’s problem in future works.